Rotated Minimum Bounding Rectangles
2024-01-19
In 2D computational geometry, rotated minimum bounding rectangles are:
- rectangles that enclose a target geometry,
- don’t (necessarily) have their sides aligned with the coordinate system axes, and
- minimise a metric (area, or the smaller of the two side widths).
I recently implemented rotated minimum bounding rectangles in the v0.47.0
release of the simplefeatures Go library. Both the minimum area and
minimum width variants are implemented. The implementation uses a rotating
calipers approach, and operates with O(n log n) time complexity.
A quick demo program to show how to access the new functionality.
package main
import (
"fmt"
"github.com/peterstace/simplefeatures/geom" // v0.47.0 or higher
)
func main() {
const input = "POLYGON((0 0,2 2,1 2,0 1,0 0))"
g, err := geom.UnmarshalWKT(input)
if err != nil {
panic(err)
}
mbr := geom.RotatedMinimumAreaBoundingRectangle(g)
// Outputs: POLYGON((0 0,2 2,1.5 2.5,-0.5 0.5,0 0))
fmt.Println(mbr.AsText())
}
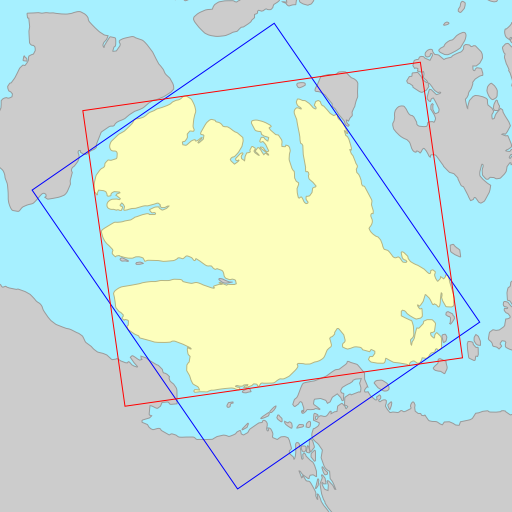
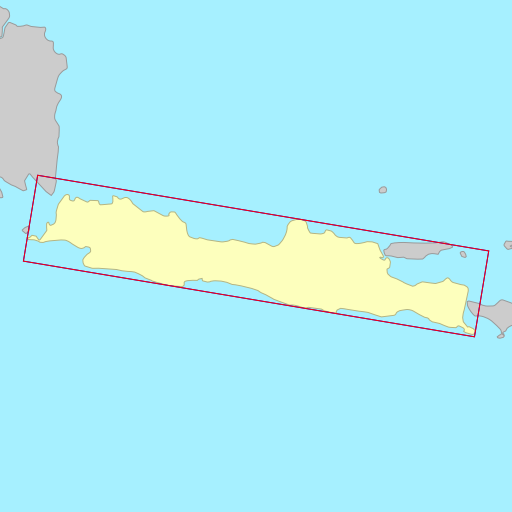
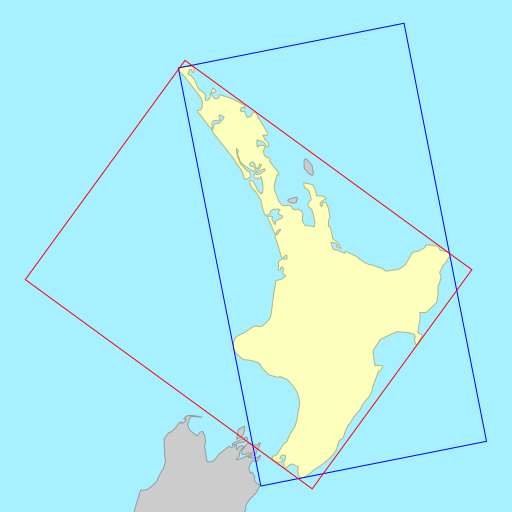
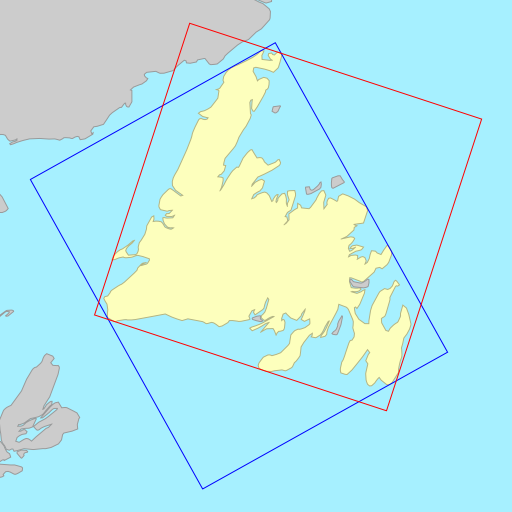
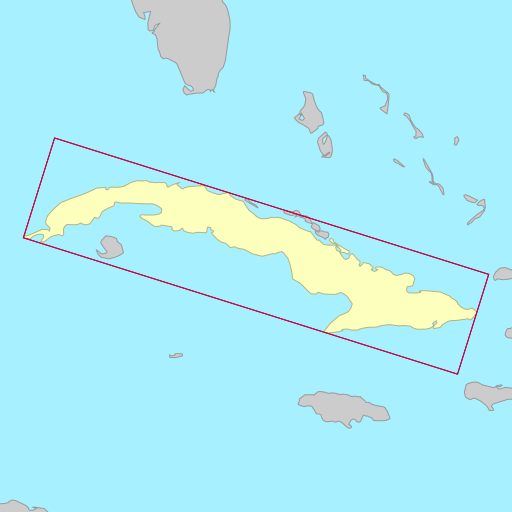
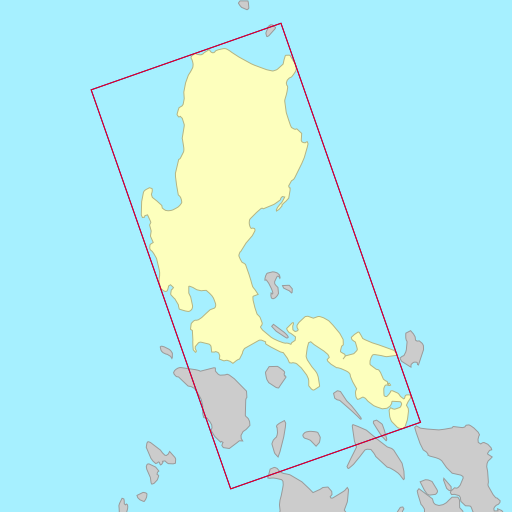
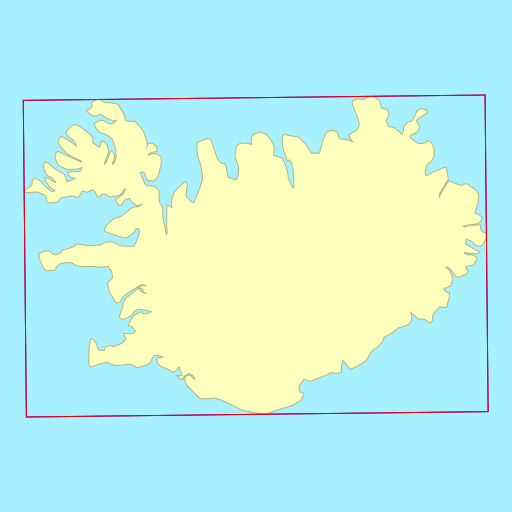
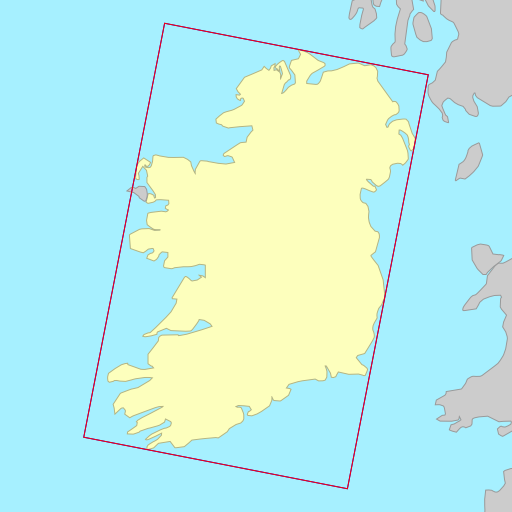
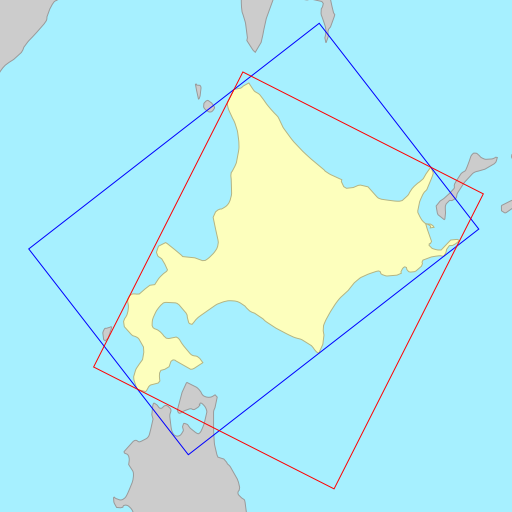
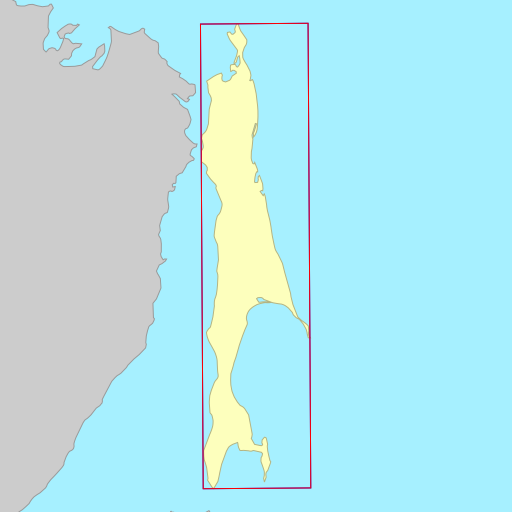
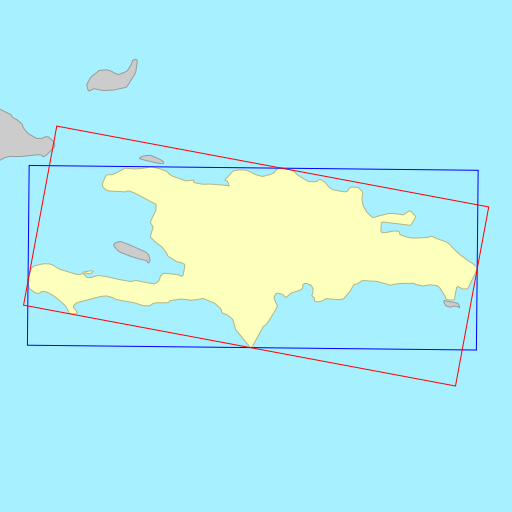
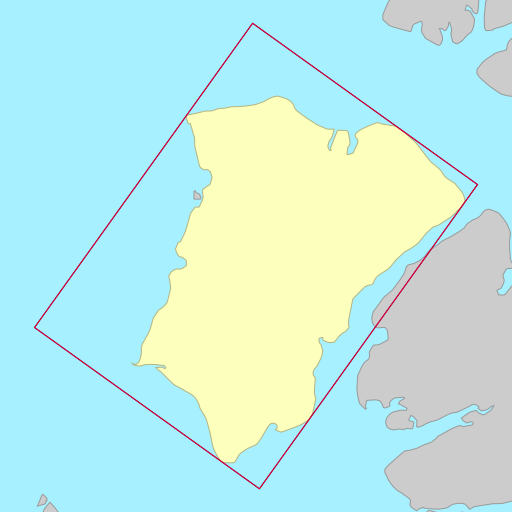
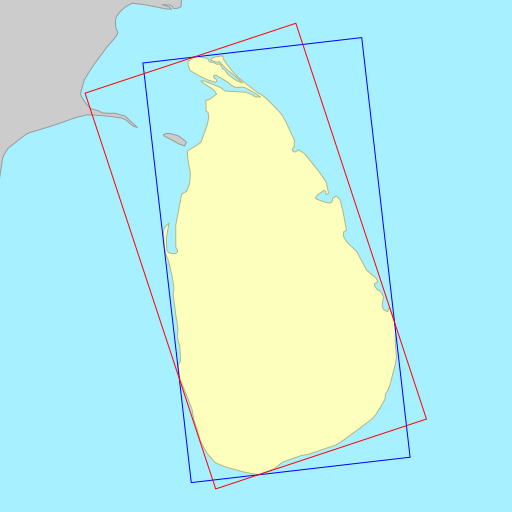
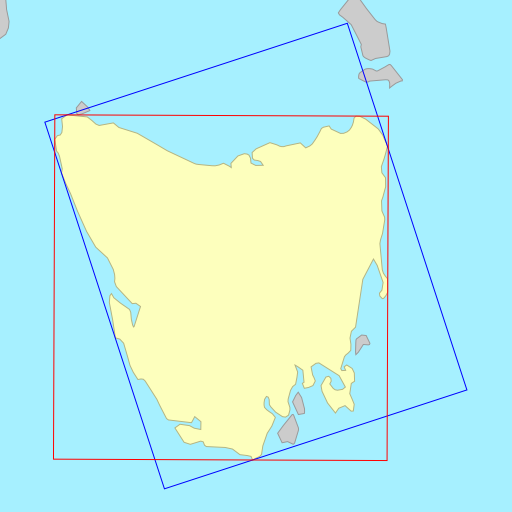
Sometimes the choice of metric to minimise (area vs. width) doesn’t matter, each resulting in a rectangle that is identical or almost identical. Other times, the choice of metric can wildly change the orientation of the rectangle.
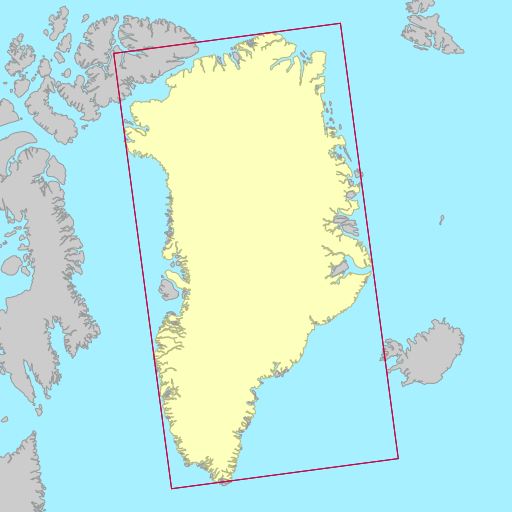
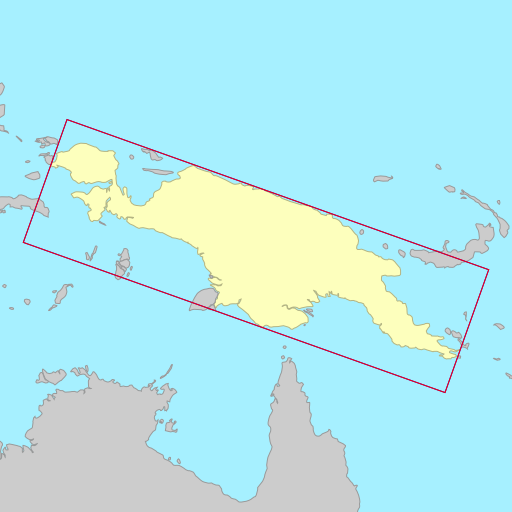
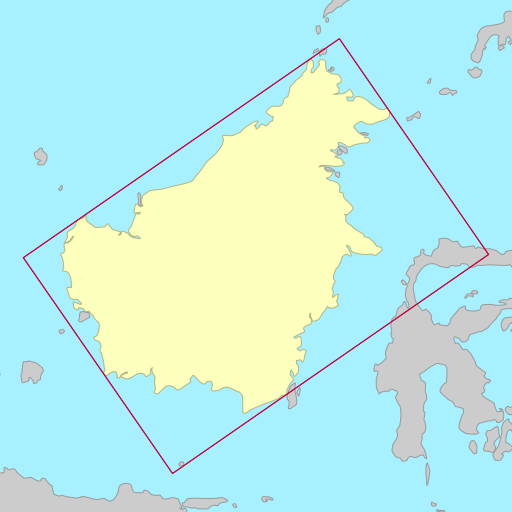
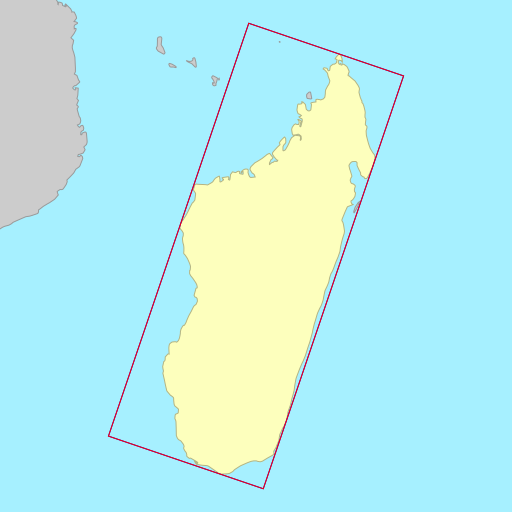
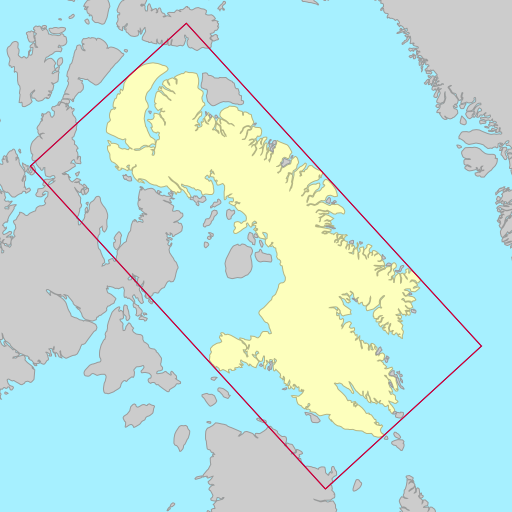
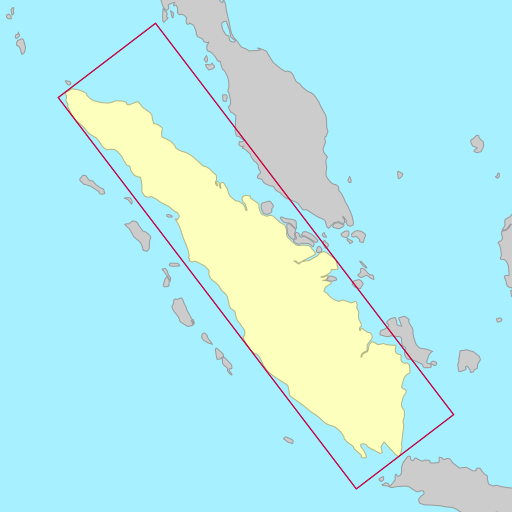
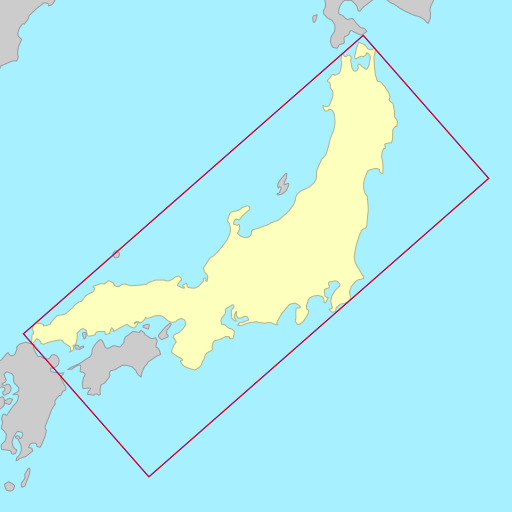
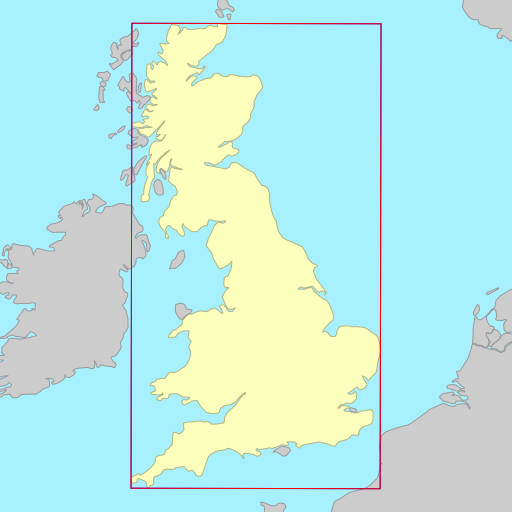
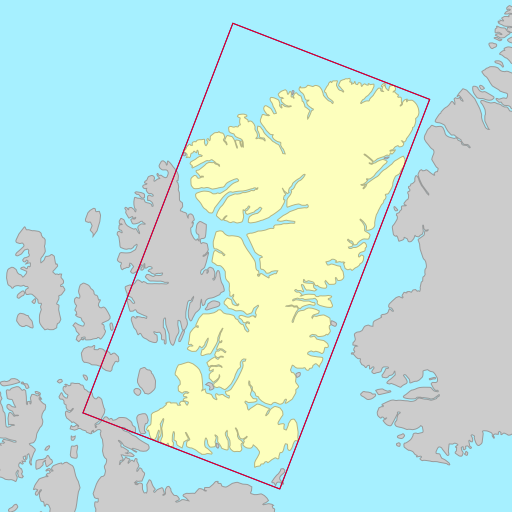
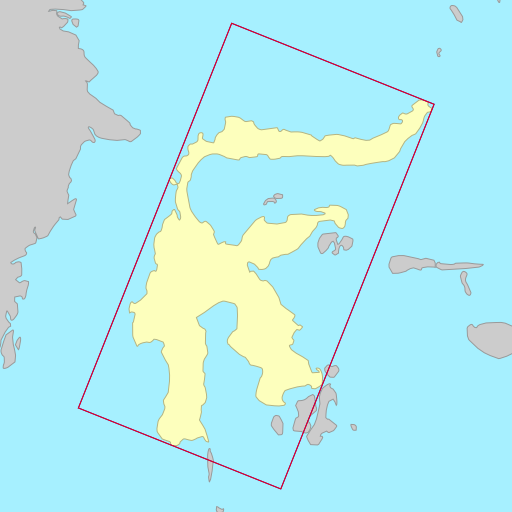
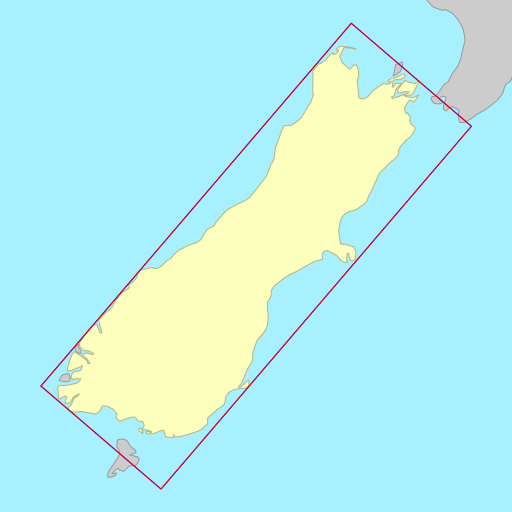
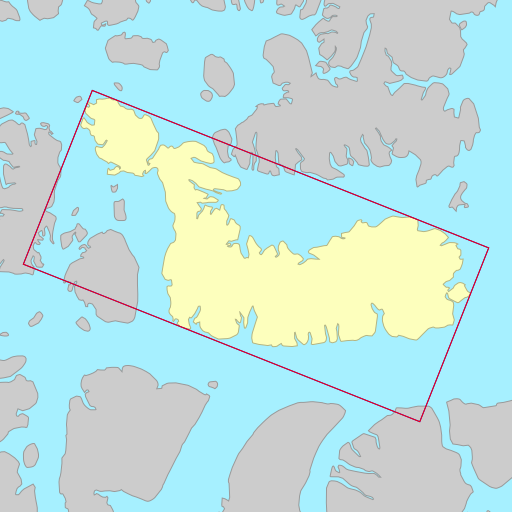
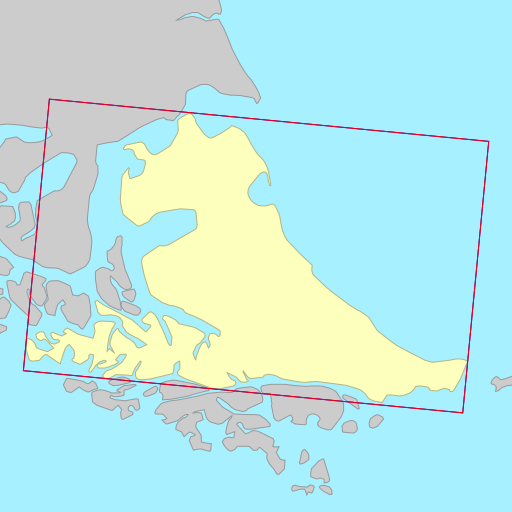
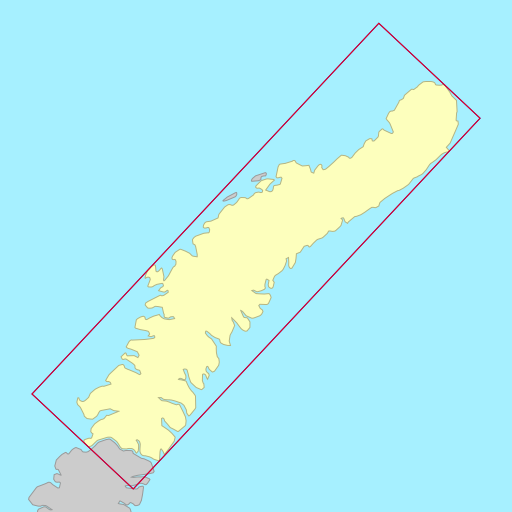
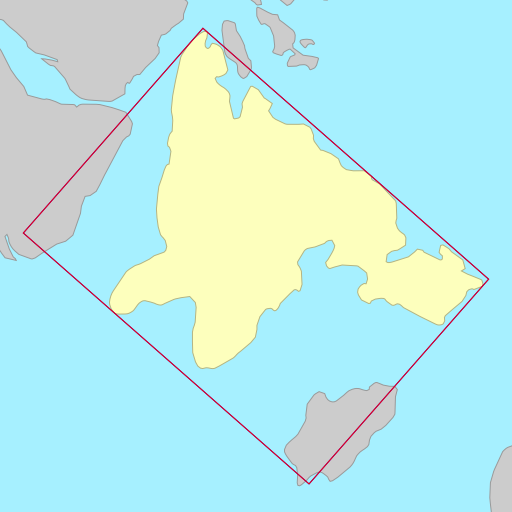
The demo below shows the rotated bounding rectangles of each of the earth’s 30
largest islands. The calculations are performed using the simplefeatures
library. The minimum area rectangles
shown in red and the minimum width
rectangles shown in blue. A lot of the time they are the same (and
overlap), but sometimes they differ considerably.